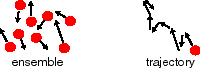DIFFUSION
What is diffusion?
Looking at many versus one
Looking at one particle: Brownian Motion
Simulation of Brownian motion
Can we see Brownian motion of a single molecule?
Einstein's contribution to our understanding of diffusion
before Einstein
x 2= 2 D t
D = R T / 6 pi N v r
Remarkable results
More thoughts on the units of D
Impact of these equations?
Brownian motion of many particles is diffusion
Simulation of diffusion
more information
Calculating the changes in concentration as diffusion progresses
Diffusion of different sized objects
Tidbits
What is diffusion?
|
|
|
|
|
|
|
Diffusion is one of the fundamental processes by which material moves. It is thus important in biology and medicine, chemistry and geology, engineering and physics, and in just about every aspect of our lives. Diffusion is a consequence of the constant thermal motion of atoms, molecules, and particles, and results in material moving from areas of high to low concentration. Thus the end result of diffusion would be a constant concentration, throughout space, of each of the components in the environment.
Of course there are also processes that generate inhomogeneity, even while diffusion is smoothing things out, and the world we live in is the sum of both. The speed of mixing by diffusion depends on three main parameters:
1. temperature
2. size (mass) of the diffusing particles
3. viscosity of the environment
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
The temperature of a system is a measure of the average kinetic energy, the energy due to movement, of the particles in the system (the distinction between particles, molecules, and atoms will not be important in our discussion). In most systems the energy is just equal to a constant times the temperature. Since a higher kinetic energy means a higher velocity, it's clear why the speed of diffusion increases with temperature: everything is moving faster (in the formula below, E is the kinetic energy, k Boltzmann's constant, T the temperature, m the mass, and v is the velocity).
A heavy particle has a lower velocity for a given kinetic energy, or temperature. A large particle interacts more with its environment, which slows it down. Thus, heavy, large particles diffuse more slowly than light, small ones.
|
|
|
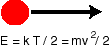 |
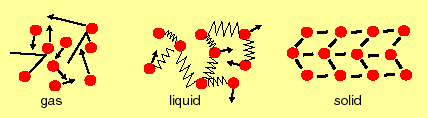
The environment (the material the diffusing material is immersed in) is very important. Diffusion is most rapid in a gas (because molecules can travel a considerable distance before they hit another molecule, and even then they just bounce off), slower in a liquid (there is a lot of movement, but all molecules remain weakly tied to each other as they move), and very slow or sometimes zero in a solid (because the forces between molecules and atoms are so generally so large that there are only infrequent exchanges of position).
Looking at many versus one
A common task is the determination of the average value of some property in a system of many particles. The property might be velocity, energy, or whatever. If we are working with a computer simulation of the system, or are trying to derive a formula to calculate the average value of this property, there are two approaches for obtaining this average:
> at one point in time, look at the entire collection of particles (the ensemble), and compute the average of the property of interest over all the particles;
> follow only one particle over a considerable time, and average the property of that particle over that time.
|
|
|
|
|
Usually these two approaches give the same result, or in statistical mechanics speak "the ensemble average is equal to the time average over the trajectory". This assumption is called the "ergodic hypothesis", and will assumed to be valid here.
Diffusion can thus be described in terms of many particles, i.e. changes in concentration of these particles as time progresses, or it can be discussed in terms of the movement of one particle. We will first focus on the behavior of a single particle, and then move on to systems with a large number of particles.
|
|
|
|
|
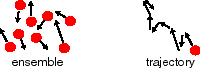 |
Looking at one particle: Brownian Motion
Robert Brown, in 1828, reported that pollen grains, when suspended in water and observed under the microscope, moved about in a rapid but very irregular fashion. In the eight decades between his description and the Ph.D. thesis of Albert Einstein in 1905, various scientists speculated about the cause of this motion. Some thought the motive power was the illumination used to see the particles in the microscope, some proposed electrical effects, and some even correctly guessed that the thermal motion, which was required by the kinetic theory of heat, was the cause. However, there was no general consensus, and little quantitative understanding of this phenomenon.
I observe Brownian motion when I look at the fluorescent, polystyrene beads that are part of the DNA diagnostic we are developing at GeneVue. These particles are only 0.5 microns in diameter (0.0005 mm) but contain over 100,000 fluorescent dye molecules, and thus appear as a very bright circles. Since their density is close to that of water, they have little tendency of sink or float, and just sit there and do the thermal dance. You can see what I see by looking at this Java simulation:
Simulation of Brownian motion
Can we see Brownian motion of a single molecule?
A molecule is generally much smaller than a polystyrene bead or a grain of pollen, and thus can not be seen in an ordinary light microscope. In such a microscope, objects are seen because they block some of the light that illuminates them from below (looking down on the object). If the object is smaller than 1/2 the wavelength of light, diffraction of light around the object eliminates most of the shadow it would otherwise cast, and we don't see it.
However, when you see an object by virtue of the light that it emits, which is the case if the object is fluorescent, refraction no longer makes it invisible. Thus you can see individual DNA molecules when they are complexed with fluorescent dyes, even though they are not visible in a normal bright field microscope because the width of the DNA helix is much smaller than the wavelength of light.
Thus, the answer to the question is yes.
Einstein's contribution to our understanding of Brownian motion and diffusion
Before Albert Einstein turned his attention to fundamental questions of relative velocity and acceleration, he published a series of papers, starting in 1905, on diffusion, viscosity, and the photoelectric effect that would have ensured him a considerable reputation even if he had not later created the Special and General Theories of Relativity.
His papers on diffusion came from his Ph. D. thesis. Diffusion had been studied extensively by that time, but was described in a completely phenomalogical framework. Einstein's contributions were to propose:
1. that Brownian motion of particles was the basically the same process as diffusion. Thus we can use the same equations for Brownian motion and diffusion, even though we look directly at the Brownian motion of a large particle, but usually measure diffusion of small molecules by following changes in concentrations.
|
|
|
|
|
|
2. a formula for the average distance moved in a given time during Brownian motion: |
|
< x 2 > = 2 D t
< x 2 > is the average value for the square of the distance
D is the diffusion coefficient
t is the time
|
|
|
|
|
|
|
|
3. a formula for the diffusion coefficient of a substance in terms of the radius of the diffusing particles or molecules and other known parameters: |
|
D = R T / 6 pi N v r
R is the gas constant (8 in SI units),
T is the absolute temperature (300 K is room temp.)
pi is 3.14159...
N is the number of molecules in a mole (6 X E23)
v is the viscosity of the solvent ( 0.001 for water in SI units)
r is the radius of the particle or molecule
|
|
Impact of these equations?
Experimental observation confirmed the numerical accuracy of Einstein's theory. This means that we understand Brownian motion is just a consequence of the same thermal motion that causes a gas to exert a pressure on the container that confines it. We understand diffusion in terms of the movements of the individual particles, and can calculate the diffusion coefficient of a molecule if we know its size (or more commonly calculate the size of the molecule after experimental determination of the diffusion coefficient). Thus, Einstein connected the macroscopic process of diffusion with the microscopic concept of thermal motion of individual molecules.
Not a bad Ph. D. thesis.
Brownian motion of many particles is diffusion
Thus we can model diffusion the same way we did the movement of a single particle, we just use more particles. In the following Java applet, we follow 16 objects as they diffuse above a surface. A second modification to the simulation is the superposition of a constant downward "drift velocity", which be can set to any value that pleases:
Simulation of diffusion
While this simulation may seen just a toy, it can be used to study some interesting situations. However, in order to use it as a quantitative tool, you need more information.
Calculating the changes in concentration as diffusion progresses
Often we are not interested in the motion of individual particles, but rather in changes in a concentration profile with time. The two differential equations that describe bulk diffusion were known well before Einstein. The 1st law is essentially the definition of the diffusion coefficient. The 1st law plus conservation of mass gives the 2nd law, and solutions of this partial differential equation are the concentration profiles resulting from diffusion.
Given the initial concentration profile, the 2nd law describes how the concentration at each position changes with time, and thus enables you to calculate the concentration profile at later times. In practice, finding the solutions of the 2nd law can be difficult. Even for simple initial concentrations, the solutions often must be expressed in terms of other "standard functions", and the numerical values extracted from tables. Here we give solutions for two of the most simple cases:
1. At t = 0 all the material is concentrated in a plane sheet at x = 0, that is arbitrarily thin (and thus the concentration in the sheet is arbitrarily large). The solution is a Gaussian distribution which becomes lower and wider as time progresses.
2. At t = 0 the concentration below the plane at x = 0 is constant, above the plane it is 0. The solution is an "S" shaped profile, the integral of a series of Gaussian curves, which becomes wider with time.
Diffusion of different sized objects
The diffusion coefficient is inversely proportional to the radius of a particle, or the cube root of the volume. So, if the mass of one spherical particle is 8 fold greater than another, its diffusion coefficient is only 2 fold smaller.
I have picked 7 chemicals, molecules, or objects (the distinction between these terms is not always clear) and calculated a (very) approximate radius (in nm), the diffusion coefficient (in SI units times 10 12 ) and the time in seconds required to diffuse 10 microns (the diameter of a typical animal cell).
| Object |
radius (nm) |
D |
time (sec) |
| oxygen |
0.2 |
900 |
0.056 |
| sucrose |
0.5 |
400 |
0.13 |
| insulin |
1.4 |
160 |
0.31 |
| ribosome |
10 |
22 |
2.3 |
| HIV |
100 |
2.2 |
23 |
| bead |
250 |
0.9 |
56 |
| bacteria |
750 |
0.3 |
170 |
This fact that I mentioned that 10 microns is the diameter of the average cell is not meant to imply that a cell is just an empty container with protein (and other) molecules bouncing around inside by diffusion. In fact, the inside of a cell is more like a scaffold, with a complex structure and machinery to transport proteins and other cellular components to specific sites. But that's another story.
Tidbits
> A recent paper on diffusion and cell-cell communication.
> Natural units.